Fiber Cleaner Tests
2024-12-08
Intro
This post is a collaboration between Hotaru, error and jo. It is published at swagspace.org as well as undefinedbehavior.de.
The idea behind this post initially came from a talk at DENOG16 about problems with return loss in optical transmission. Our question was: How dirty do fibers get and how much work is it to get them clean again.
Making fibers dirty
We primarily tested two different kinds of contamination. The first kind is touching the fiber. The second kind is contamination with dirt, e.g. from the floor. Both kinds can happen easily when handling fiber.
It is interesting to see how visually distinct the different kinds of contamination are. Just touching the polished face of the fiber once with our fingers covered the whole face with a thin grease film.

Swiping over the face of the fiber leads to a more streaky pattern.

The contamination when touching hair is very similar to touching the fiber with your fingers.
Dropping the fiber on the floor (in our case a carpet) contaminates the fiber with many small pieces of dirt.

Different types of cleaners
Click-Cleaners
Click-Cleaners are somewhat pen shaped and fit directly on top of the connector of the fiber. By pushing down on them, a small cleaning thread is dragged over the face of the fiber, cleaning it in the process. Afterwards, a spring pushes the cleaner back into it's original position, ready to be used again.
Manual swiping
Manual swiping cleaners have a button that exposes a piece of cleaning cloth when pressed. The fiber can then be swiped over the cloth to clean it. When the button is released, the cover closes and the microfiber cloth moves forward.
Miscellaneuos "cleaning utensils"
Sometimes you have to improvise. What if you don't have professional cleaning utensils at hand? So we looked at wether a pair of work trousers and a piece of cleaning cloth for glasses work, as well as unicorn Ida and the locomotive Chuff Chuff.
Tests
We did several tests with each type of cleaner and different kinds of contamination. We cleaned until the fibers passed IEC 61300-3-35 testing. The standard defines 4 areas of the fiber. The core (A), cladding (B), a small glue area (C) and the contact area of the ferrule (D). The test specification allows for some minor defects on the fiber, especially in the contract area. So there might be some contamination left. Keep this in mind when looking at the figures.
We used an EXFO FIB430B video microscope with automatic analysis features to analyse the fibers.
All our tests were done on Singlemode LC/UPC connectors.
Cletop S

The Cletop S is based on manual swiping. In all 4 tests the Cletop S cleaned the fiber after one swipe.
Senko Smart Cleaner

The Senko Smart Cleaner is of the click cleaner variety. In our tests we had the issue, that this cleaner did not reliably clean the fiber. It looks like some part of the fiber did not get wiped at all.
This is an example of a dirty fiber before cleaning

And this is the result of the first cleaning.
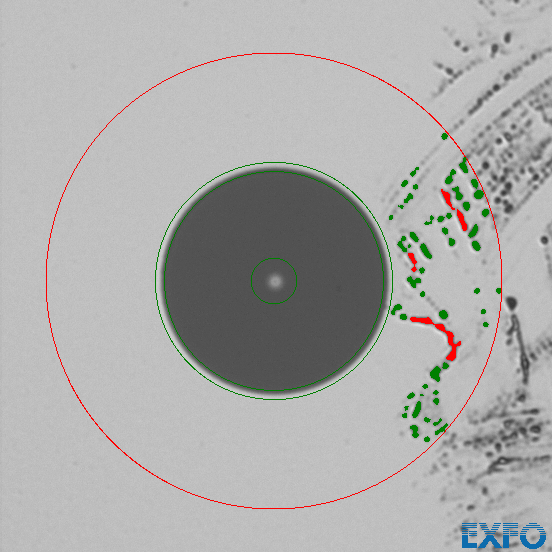
We have seen this pattern multiple times with this device during our tests. 3 clicks were necessary in order to reliably clean the fibers.
IBC Brand Cleaner Zi125

This cleaner is also of the click cleaner variety. In all but 1 of our 4 tests this cleaner cleaned the fiber in one click. In the one attempt that didn't clean the fiber, we observed a piece of contamination being moved onto the fiber that wasn't there before.

This is the uncleaned fiber. (Note: This fiber passed the IEC test, because the contamination is small enough.) After cleaning this fiber a large piece of contamination was moved into the contact area that was not on our fiber before (or at least not in the part that we were able to observe with out microscope).

Here we can see a large piece of contamination in the top center. Cleaning it once again removed the defect.

This shows us, that it is possible to introduce new defects through cleaning.
Other cleaning utensils
We had several other "improvised cleaning utensils" at hand so we did a couple of quick tests. Hold on tight, we are entering shitpost territory now.
Work trousers and microfiber cloths for glasses
We did a quick test on a pair of work trousers that were worn for several days. The results were not great.


The trousers were not able to get the fiber clean, not even after several swipes. The other issue with potentially contaminated pieces of clothing is, that you might introduce new contamination.
We tried the same with used microfiber cloth for glasses.

Technically this fiber is clean according to the standard. However there is a significant chance, that the defects still on the fiber end up in the center of the fiber. So we can't recommend this method.
Plushies
In case you are carrying your plushy companion into the datacenter or the field, they might help you cleaning fibers. We did tests with multiple different kinds of surfaces on Chuff-Chuff, a locomotive plushie. Unfortunately none produced good results.
However the results that were produced by unicorn Ida were surprisingly good.

Ida got the fiber almost clean with the first swipe:

There is only one piece of contamination. Sadly that one is directly in the center of the fiber where no contamination is acceptable. Further swipes were not able to remove this contamination. (A purpose-built cleaner did it first try).
Conclusions
- Making fibers dirty is surprisingly easy. Simply dropping them on the ground or touching them is sufficient.
- The Cletop S and IBC Brand Cleaner usually cleaned the fiber in 1 swipe/click, 2 at most.
- If you are not working on very critical optical interfaces 1 swipe on a cletop or 2 clicks from a good cleaner are sufficient.
- It doesn't occur frequently, but it is possible to reintroduce dirt to the contact area of a fiber from other parts through cleaning. If you are working on critical patches, use a scope to verify your work.
- Keep in mind, that this is a limited test on LC-PC/UPC connectors only and that we are only testing the patch cable end of the interface. The results might not hold for other types of connectors like E2k, SC or the APC variants of these connectors.
- Due to missing equipment we were not able to test the cleaning performance of the click cleaners in the recepacle part of the connection, e.g. a transceiver.
Self-made Tarp
2024-07-30

Every now and then I am on some sort of camping event or festival. And when you are a large group you want to have some sort of shared space where you can sit, cook, talk, cuddle, store electronics or your camping chair and get out of the sun or rain.
Cheap folding pavilions are readily available, however they are usually only 3x3m or 3x6m meters and rather shitty. They break after a couple of events and repairing them is hard. Spares are usually not available. There are better versions available, but those are expensive.
There are also party tents, but those are usually also expensive if you want to have the good stuff and often have tent poles that are 2m long. Those poles don't fit in regular cars. You need some sort of van to get those to places.
Finally there are tarps. I like tarps, because they are open to all sides which makes them rather welcoming. This also leads to some ventilation. There are many small tarps in the 3x3m to 4x4m range, but those are usually to small. There are bigger versions that are designed as stretch tents. They look really nice with their stretchy fabric and can be set up in different shapes. But those usually cost thousands of euros as well.
So, let's try to hack something that is rather cheap, strong, can be fixed/has spare parts available and fits into regular cars.
A tarp is probably the easiest thing to build, so that's what I did. You basically need:
- the tarp itself
- some poles to lift the tarp of the ground
- tent pegs and some sort of guy line
The Tarp itself
Initially I wanted to have a tarp similar to the tarp used on trucks. That stuff is usually made from PVC and weighs somewhere between 600 and 900g/m^2. It is also rather expensive (~150-200€ for 5x6m).
A somewhat cheaper option is a Polyethylene (PE) tarp. That is what the usual plastic tarps you probably know are made of. The ones you get in your hardware store are usually around 90g/m^2, sturdier ones might have 120g/m^2. Those are thin, break easily and not really confidence inspiring. However there are more robust versions available. I got one with 300g/m^2 which costs ~60€ for the 5x6m version. This is the heaviest version made from PE that I found. I might upgrade to the PVC ones when the concept works and the PE one is worn out.
The Poles
There are tarp poles that are readily available. However most of them are designed for small (think 3x3m) and light cloth tarps. My PE tarp weighs almost 10kg and a PVC version will be even heavier. so small and flimsy poles are out. The other problem is, that the poles need to be high enough so that people can stand under the tarp. My goal was that most people can enter through all sides. This means 1.8m should be the minimum height of the poles. To get some slope I needed at least an additional 0.5m for the larger poles. So I needed 2 poles that are at least 2.3m in height, more should be better. That rules out a lot of the remaining ready made poles.
In the end I settled for some old poles that were used by the German military to prop up camo netting ("Tarnnetzaufstellstangen"). Those can be found on eBay and army shops in Germany and are available in lengths of 1.2m, 0.6m and 0.3m + 0.1m for a coupling section. Those poles are ~4cm in diameter and made out of fiber-reinforced plastic. They can be coupled to build longer poles. I bought some of the 1.2m and 0.3m poles, because the 0.6m poles are rather rare and expensive. This gave me 2.5m for the long poles (2x1.2, + 0.1 for the connection piece) and 1.9m (1.2m + 2x0.3m + 0.1 for the remaining connection piece) for the short ones
In the end I payed ~100€ for the poles.
Now I need a way to attach the poles to the tarp. I got access to the wood lathe of a friend to build some wooden end caps for the poles. They are from cheap wood I already had. I added a steel pin into the end cap that can be inserted into the grommets of the tarp.


The Tent pegs and guy line
This tarp is rather large and has to withstand more force that a regular tarp. It also requires more force to tension it.
I decided to use large 30cm T-shaped tent pegs. I might have chosen larger ones, but the campground at CCCamp23 permitted only 30cm. (The tarp wasn't at CCCamp23 in the end...) And nothing stops me from replacing them later. To drive those pegs in I am using a small 2kg hammer. I also tried a smaller 600g hammer, but it takes forever.

For the guy lines I got inspired by bigger tents. Those often use ratchet straps. I decided to use cheap ratchet straps that are rated for 400kg which should be sufficient. I assume that something else breaks before the ratchets break.
The tent pegs did cost ~35€ and ~25€ for the ratchets.
First setup
The first time I set this up I used a small patch of grass on a playground in my neighborhood. The setup works well with 2 people.
The way to do it is:
- lay out the tarp
- build the poles
- lay the poles on the ground, starting at the grommets of the tarp, facing outwards in the direction the ratchet straps will face.
- drive in the tent pegs at the end of the poles.
- prepare the ratchets traps. If you insert the strap into the ratchet and tighten it just far enough that both segments of the strap overlap in the ratchet you can still tighten the strap by pulling on one end, but it stays in place when under slight tension. You can still cinch it down later with the ratchet. This is useful for a quick and easy setup.
- start by raising the first of the two long poles, tighten the strap, so that the pole is upright.
- Then one person has to hold that pole upright while an other one raises the opposing long pole and tightens it. When properly tightened one person holding one pole was sufficient to keep the tarp upright.
- then add both of the corners on one side. This should makes the tarp stable enough to stand by itself.
- then add the remaining poles
- make minor adjustments to the placement of the poles
- tighten the straps properly.
After this procedure we had a standing tarp.

In this picture the poles on the far side are only 1.6m high while the ones on the front are 1.9m high because I did not have enough 30cm pole pieces.
Issues of the first setup and further improvements
One issue that I expected was that the middle might be sagging a bit and it did. So I had one further pole without a metal spike on the end and we added that one in the middle. It improved the sagging a lot.
An other issue was that the grommets were not intended for the amount of force the ratchets put into them via the metal pins of the poles. The metal grommets got bent and they might separate from the tarp and wouldn't last very long. The issue here is that the force is distributed over a small piece of the tarp. To improve this I bought some strap. That was sewn onto the tarp to distribute the load. Doing this with a sewing machine was impossible, because I could not handle a 5x6m tarp in the sowing machine. It was simply to big, sturdy and heavy.
So after a lot of hand-sewing I had 4 loops on my tarp. I left out the corners as they were, because these had additional corner reinforcements and looked fine.

The ratchet straps also got an improvement. Initially I set them up as loops that wrap around the pole and the tent peg. I changed that. I cut off the strap 1m after the ratchet and tied a loop in the strap. Now they can be wrapped around the tent pegs. The remaining strap got a loop as well which can simply be hung over the pin in the pole. This also makes tensioning easier, because in the previous setup the strap could slip of the tent peg.

The straps were also inspected by professionals:

Second setup at FAT24
The first time the tarp actually got used was at FAT24.
The build up went smoothly with 3 people.
One issue we had was that the ground was rather soft and had several former molehills. We drove the pegs in to far vertically and they got pulled out a bit when tightened. We fixed that by placing them in better spots and driving them in at an angle.
An other issue with the soft ground was that the poles could sink in when under load. During the first test build up a friend of mine could climb up the pole and it carried the load just fine. This time the ground was soft and the pole sank ~10cm into the ground.
I will fix that by adding some sort of ground plate with a small divet in it to place the end of the pole into. This should distribute the load over a larger area.
We also realized, that the tarp is strong in all directions, but moves a bit more in rotation around the center pole. It is probably sufficient, because the tarp should not see a rotational force and the straps will eventually take the load. However using 2 straps on the corners in line with the adjacent edges instead of one strap diagonally outwards should improve this. So I ordered more ratchet straps and tent pegs.
Once the tarp was set up we wrapped the loose ends of the straps around the ratchets which gave it a really clean look. And we added some lights.


The tarp held up well during FAT24. It stayed dry during the rain and offered some shade. Build up, tear-down and the logistics involved worked fine. So this tarp will make it's way with further improvements to other events.
The Lamp Part 1: The Prototype
2024-07-21
When I was young my aunt had a lamp with 2 knobs that would change the color of the lamp. I think she still has that lamp. I am not sure how that lamp worked. But it must be at least 20 years old, so I assume, that inside there must be a regular light bulb and the knobs move colored filters in front of the bulb. Maybe I should check out that lamp the next time I visit my aunt.
Anyways: I really like the lamp with the knobs, and I am cheap, so I will build a clone and RGBWW LED rings it is!
Hardware
The hardware is rather cheap, just a Raspberry Pi Pico, because that's what I had at hand and a small 16 LED WS2812 RGBWW LED ring and 3 potentiometers. The potentiometers are connected to the 3 ADCs of the Pico. The LEDs are powered directly from the VBUS pin on the Pico.
The actual body of the lamp is a problem for later. First I have to get the software running.
Software
Initially I wanted to use Rust, but embedded Rust, the RP2040 HAL/BSP/etc. ecosystem and I once again got stuck in dependency hell. So I decided to go back to MicroPython, which works just fine.
The code is rather trivial.
The potentiometers are read via the ADCs. The ADCs are then mapped to a range from 0 for 1. However the values are somewhat noisy and don't truly reach the ends of the voltage spectrum. So I clipped the upper and lower end of the spectrum a bit and scaled the remainder. After that the output was still somewhat noisy, so I decided to dampen that by adding some exponential smoothing;
1 potentiometer is mapped directly to the white value, while the other 2 are used as the Hue and Value in the HSV color model which is then translated to RGB.
So far this works quite well. Here is a picture of what the breadboard setup looks like:

An Overview and Cheat Sheet for systemd networkd configurations
2023-09-23
This is a short cheat sheet for things that I often need to do with systemd-networkd, the network configuraton component of systemd. This post assumes some basic knowledge about systemd-networkd and is primarily a collection of examples.
CLI overview
The CLI tool for systemd-networkd is networkctl.
networkctl shows a short status over all interfaces
networkctl reload reloads and applies the configuration of all interfaces.
networkctl status shows a general status as well as the logs.
Check the logs if something does not work as intended.
Syntax errors and the like are logged here.
The logs can also be accessed via the journal, usually with journalctl -xef -u systemd-networkd
Configuration Files
systemd-networkd is configured via files usually located in /etc/systemd/network/.
There are 3 kinds of files
.link-files that are used for renaming interfaces (Documentation).netdev-files that are creating interfaces (Documentation).network-files that handle the L3-behaviour of those interfaces (Documentation)
The files are loaded sorted by their name, so it is a good practice to name them starting with numbers to define their order.
Interface renaming
To rename a interface we can first match on some parameters and then give it a new name:
# 00-iface42.link
[Match]
MACAddress=11:22:33:44:55:66
Type=ether
[Link]
Name=iface42
The Type=ether is important when you want to create VLAN interfaces on the
renamed interface.
By default the VLAN Interfaces would have the same MAC addresses as the main
interface.
If only the MAC address is matched then the main interface and the VLAN interfaces
would all be renamed, leading to hard to find errors.
The Type=ether matches only on the ethernet interface, because the VLAN interfaces
have vlan as their type.
Source: systemd-devel mailing list
VLAN Interfaces
First we have to create the VLAN Interface eth1.102 and assign it the VLAN-ID 102
# 10-eth1.102.netdev
[NetDev]
Name=eth1.102
Kind=vlan
[VLAN]
Id=102
Note that the name of the interface can be chosen arbitrarily and does not have to contain the vlan id.
Then we can assign the VLAN to an other interface:
# 10-eth1.network
[Match]
Name=eth1
[Network]
VLAN=eth1.102
VRFs
Each VRF needs a routing table assigned to it. In this example it is table 102.
# 10-vrf-uplink-1.netdev
[NetDev]
Name=vrf-uplink-1
Kind=vrf
[VRF]
TableId=102
To bring the VRFs up you need a network file for them. You can use the same file for all your VRFs. An easy example would be
# 99-vrf.network
[Match]
Kind=vrf
[Link]
ActivationPolicy=up
RequiredForOnline=no
Some manuals suggest to match the name here, e.g. Name=vrf-*,
however this requires all your vrfs to start with vrf- which might not be
the case.
To assign an interface to a VRF, create a network file for that interface:
# 20-eth2.network
[Match]
Name=eth2
[Network]
VRF=vrf-uplink-1
Assigning IP Addresses
SLAAC + DHCP
To run SLAAC for IPv6 and DHCP for legacy IP a network file is added:
[Match]
Name=eth0
[Network]
DHCP=yes
IPv6AcceptRA=yes
IPv6PrivacyExtensions=yes
The handling of IPv6 RAs is a bit complicated, check the documentation for IPv6AcceptRA for details.
The IPv6PrivacyExtensions=yes enables IPv6 privacy extensions.
The set the route metric (this is relevant if you have multiple interfaces and e.g. want to prefer your wired over your wireless interface) add the following lines:
...
[DHCPv4]
RouteMetric=200
[IPv6AcceptRA]
RouteMetric=200
Static Addresses
[Match]
Name=wg-1
[Network]
Address=2a0a:4587:2001:1015::/127
Routes
Static routes can be added with the [Route] config section in the network
files.
To add more routes, simply add more [Route] config sections.
[Route]
Destination=10.42.123.0/28
Gateway=192.0.2.1
[Route]
Destination=2001:db8:101::/46
Gateway: 2001:db8::1
Wireguard Tunnels
For Wireguard a keypair is needed which can be generated with
mkdir -p /etc/wireguard
cd /etc/wireguard
wg genkey | tee privatekey | wg pubkey > publickey
Then the netdev looks like this
[NetDev]
Name=wg-1
Kind=wireguard
[WireGuard]
PrivateKeyFile=/etc/wireguard/privkey
ListenPort=51820
# for a client we only want to listen for but not actively connect to
[WireGuardPeer]
PublicKey=<peers public key here>
AllowedIPs=::/0, 0.0.0.0/0
# for a peer to which we want to connect to
[WireGuardPeer]
PublicKey=<peers public key here>
AllowedIPs=::/0, 0.0.0.0/0
Endpoint=[2001:db8::1234]:51821
Additionally a network file is needed:
[Match]
Name=wg-1
[Network]
Address=172.16.44.1/31
Zyxel NR7101 Performance Testing
2023-05-11
Introduction
The Zyxel NR7101 is a PoE-powered 5G router. It is often used to gain internet connectivity for LAN parties. This leads to large volumes of traffic going through the device. Some events reported reliability issues with this device. So we will investigate where the limitations of this device are.
Test-Setup
We connect our test client (in this case a computer running Linux) via Ethernet to the Zyxel router. That router then connects via LTE or 5G to the Broadband ISP (in this case Deutsche Telekom). For some of the tests we require a test server with internet connectivity to send packets from the internet to our test device.
It must be acknowledged, that some of the tests might be influenced by the network of the broadband ISP, however in some cases we can clearly show, that there is a limitation on the Zyxel router.
Accessing the Web-UI
The device can be configured via a Web UI. This can be done via the wireless network that this device creates or via a Ethernet connection.
From there we can configure many settings. Especially interesting for our purposes is setting the APN under Network Setting -> Broadband -> Cellular APN to a APN which gives us a public IPv4 address so that we do not have Carrier Grade NAT. An other important option is to enable IP Passthrough, so that that our test client actually gets the public IPv4 address and the router does not introduce an additional layer of NAT.
The web UI also offers an overview over many of the signal characteristics. An explanation of these values can be found in the Zyxel support portal
Finally the device can also be accessed via SSH. To do so one has to activate SSH via the Maintenance -> Remote Management Menu. Then we can log into the device via SSH with the user admin and the same password that is also used for the web UI. Your SSH client might be very new, so you might have to enable ssh-rsa as a the host key algorithm to log in.
ssh root@192.168.1.1 -o HostKeyAlgorithms=+ssh-rsa
However the SSH login only gives you access to a very minimalistic, proprietary CLI interface.
Gaining root access
Since the regular SSH login is very limited we can get a root login. The router generates it's root password from it's serial number. More details on how to generate that password can be found at the OpenWrt Wiki.
Equipped with this root password we have access to the Linux OS running on the device.
BusyBox v1.20.1 (2022-11-29 09:28:07 CST) built-in shell (ash)
Enter 'help' for a list of built-in commands.
_______ ___ ___ _______ _____
|__ |.--.--.| | || ___|| |_
| __|| | ||- -|| ___|| |
|_______||___ ||___|___||_______||_______|
|_____|
-------------------------------------------
Product: NR7101
Version: 1.00(ABUV.7)C0
Build Date: 2022/11/29
-------------------------------------------
root@NR7101:~#
It is a small Linux system, that runs the standard Linux networking stack. So you will find netfilter, iptables, iproute2, conntrack, tcpdump, etc.
General commands
Here is an overview of the available commands:
root@NR7101:~#
8021xd date gunzip mailsend pure-ftpd syslog-ng wan
8021xdi dbclient gzip makedevlinks.sh pwd syslogd watch
AutoSpeedTest dd halt md5sum qimeitool sysupgrade watchdog
Ethctl depmod head microcom qmi-network tail wc
QFirehose df hexdump mii_mgr qmicli tar wget
SpeedTest dhcp6c hostid mkdir quectel-CM taskset which
[ dhcp6relay hostname mkfifo quectel-DTool tc wifi
[[ dhcp6s hotplug-call mknod quectel_qlog tcpdump wifi_led.sh
ac diag_start.dat httpdiag mktemp radvd tee wifi_off_timer.sh
acl diff hwclock modprobe ramonitor telnet wlan
agetty dirname hwnat more readlink telnetd wlan_wps
arping dmesg hwnat-disable.sh mosquitto_pub reboot test xargs
ash dns hwnat-enable.sh mosquitto_sub redirect_console tftp yes
atcmd dnsdomainname id mount reg time zcat
ated dnsmasq ifconfig mpstat reset top zcmd
atftp drop_caches.sh init mtd_write restoredefault touch zebra
awk dropbear insmod mtr rilcmd tr zhttpd
basename dropbearkey ip mv rilcmd.sh traceroute zhttpput
bcm_erp.sh du ip6tables nc ripd traceroute6 zpublishcmd
blkid ebtables ip6tables-restore ndppd rm true zstun
brctl echo ip6tables-save netstat rmdir tty2tcp zsuptr69
btnd egrep ipcalc.sh nice rmmod tty_log_echo zsuptr69cmd
bunzip2 env iperf3 nslookup route ubiattach ztr369cmd
busybox esmd iptables ntpclient rs6 ubiblock ztr69
bzcat eth_mac iptables-restore ntpd scp ubicrc32 ztr69cli
cat ethwanctl iptables-save nuttcp sed ubidetach ztr69cmd
cfg expr iwconfig nvram self_check.sh ubiformat ztzu
chgrp ez-ipupdate iwlist nvram-factory sendarp ubimkvol zupnp
chmod false iwpriv obuspa seq ubinfo zupnp.sh
chown fdisk kill obuspa.sh setsmp.sh ubinize zybtnchk
chpasswd fgrep killall openssl sh ubirename zycfgfilter
chroot find klogd opkg sleep ubirmvol zycli
clear firstboot led.sh passwd smp.sh ubirsvol zyecho
cmp flash_mtd less pgrep snmpd ubiupdatevol zyecho_client
config.sh free ln pidof sort udhcpc zyledctl
conntrack fsync logger ping speedtest udpst zysh
conntrackd ftpget login ping6 ss umount zywifid
cp ftpput login.sh pings start-stop-daemon uname zywifid_run.sh
crond fuser logread pingsvrs switch uniq zywlctl
crontab fwwatcher logrotate pivot_root switch_root updatedd
curl genXML ls poweroff swversion uptime
cut getty lsmod pppoectl sync vcautohuntctl
dalcmd gpio lsof printf sys vconfig
dat2uci grep lte_srv_diag ps sysctl vi
Interfaces
The interface configuration looks like this:
1: lo: <LOOPBACK,UP,LOWER_UP> mtu 65536 qdisc noqueue state UNKNOWN group default
link/loopback 00:00:00:00:00:00 brd 00:00:00:00:00:00
inet 127.0.0.1/8 scope host lo
valid_lft forever preferred_lft forever
inet6 ::1/128 scope host
valid_lft forever preferred_lft forever
2: ifb0: <BROADCAST,NOARP> mtu 2048 qdisc noop state DOWN group default qlen 32
link/ether 2e:c1:bf:ac:dd:3a brd ff:ff:ff:ff:ff:ff
3: ifb1: <BROADCAST,NOARP> mtu 2048 qdisc noop state DOWN group default qlen 32
link/ether c6:b6:cb:33:53:e7 brd ff:ff:ff:ff:ff:ff
4: eth2: <BROADCAST,MULTICAST,UP,LOWER_UP> mtu 1500 qdisc pfifo_fast master br1 state UNKNOWN group default qlen 1000
link/ether 4c:c5:3e:a3:79:e2 brd ff:ff:ff:ff:ff:ff
inet6 fe80::4ec5:3eff:fea3:79e2/64 scope link
valid_lft forever preferred_lft forever
5: usb0: <NOARP,UP,LOWER_UP> mtu 2048 qdisc pfifo_fast state UP group default qlen 1000
link/ether 02:50:f4:00:00:00 brd ff:ff:ff:ff:ff:ff
inet6 fe80::50:f4ff:fe00:0/64 scope link
valid_lft forever preferred_lft forever
6: wwan0: <NOARP,UP,LOWER_UP> mtu 1500 qdisc pfifo_fast state UNKNOWN group default qlen 1000
link/ether 02:50:f4:00:00:00 brd ff:ff:ff:ff:ff:ff
inet6 fe80::50:f4ff:fe00:0/64 scope link
valid_lft forever preferred_lft forever
7: wwan1: <NOARP> mtu 1500 qdisc noop state DOWN group default qlen 1000
link/ether 02:50:f4:00:00:00 brd ff:ff:ff:ff:ff:ff
8: wwan2: <NOARP> mtu 1500 qdisc noop state DOWN group default qlen 1000
link/ether 02:50:f4:00:00:00 brd ff:ff:ff:ff:ff:ff
9: wwan3: <NOARP> mtu 1500 qdisc noop state DOWN group default qlen 1000
link/ether 02:50:f4:00:00:00 brd ff:ff:ff:ff:ff:ff
10: wwan4: <NOARP> mtu 2048 qdisc noop state DOWN group default qlen 1000
link/ether 02:50:f4:00:00:00 brd ff:ff:ff:ff:ff:ff
11: wwan5: <NOARP> mtu 2048 qdisc noop state DOWN group default qlen 1000
link/ether 02:50:f4:00:00:00 brd ff:ff:ff:ff:ff:ff
12: wwan6: <NOARP> mtu 2048 qdisc noop state DOWN group default qlen 1000
link/ether 02:50:f4:00:00:00 brd ff:ff:ff:ff:ff:ff
13: wwan7: <NOARP> mtu 2048 qdisc noop state DOWN group default qlen 1000
link/ether 02:50:f4:00:00:00 brd ff:ff:ff:ff:ff:ff
14: teql0: <NOARP> mtu 1500 qdisc noop state DOWN group default qlen 100
link/void
15: ra0: <BROADCAST,MULTICAST,UP,LOWER_UP> mtu 1500 qdisc pfifo_fast master br0 state UP group default qlen 1000
link/ether 4c:c5:3e:a3:79:e3 brd ff:ff:ff:ff:ff:ff
inet6 fe80::4ec5:3eff:fea3:79e3/64 scope link
valid_lft forever preferred_lft forever
16: eth3: <BROADCAST,MULTICAST> mtu 2048 qdisc noop state DOWN group default qlen 1000
link/ether 00:0c:43:28:80:03 brd ff:ff:ff:ff:ff:ff
17: br0: <BROADCAST,MULTICAST,UP,LOWER_UP> mtu 1500 qdisc noqueue state UP group default
link/ether 4c:c5:3e:a3:79:e2 brd ff:ff:ff:ff:ff:ff
inet 192.168.1.1/24 brd 192.168.1.255 scope global br0
valid_lft forever preferred_lft forever
inet6 fe80::4ec5:3eff:fea3:79e2/64 scope link
valid_lft forever preferred_lft forever
18: apcli0: <BROADCAST,MULTICAST> mtu 2048 qdisc noop state DOWN group default qlen 1000
link/ether 4e:c5:3e:03:79:e3 brd ff:ff:ff:ff:ff:ff
19: br1: <BROADCAST,MULTICAST,UP,LOWER_UP> mtu 1500 qdisc noqueue state UP group default
link/ether 4c:c5:3e:a3:79:e2 brd ff:ff:ff:ff:ff:ff
inet 37.83.118.29/30 brd 37.83.118.31 scope global br1
valid_lft forever preferred_lft forever
inet6 fe80::4ec5:3eff:fea3:79e2/64 scope link
valid_lft forever preferred_lft forever
And since there are also bridges, here is the bridge configuration.
root@NR7101:/usr/sbin# brctl show
bridge name bridge id STP enabled interfaces
br0 8000.4cc53ea379e2 no ra0
br1 8000.4cc53ea379e2 no eth2
The important parts here are:
- wwan0: The first WWAN interface.
- eth2: The Ethernet link that we are using to connect to the device. This is connected to br1.
- br1: The bridge interface over which we access the device via eth2.
- br0: The bridge for the wireless LAN network of the device.
- ra0: the actual wireless interface that is connected to br0.
Routing Table
The routing table is also rather straight forward:
root@NR7101:/usr/sbin# ip route
default dev wwan0 scope link src 37.83.118.29
37.83.118.28/30 dev br1 proto kernel scope link src 37.83.118.29
127.0.0.0/16 dev lo scope link
192.168.1.0/24 dev br0 proto kernel scope link src 192.168.1.1
239.0.0.0/8 dev br0 scope link
First we have the default route as a onlink-route. Then the local networks on the bridges br1 and br0 and the loopback interface. And somehow it also adds a multicast network to the bridge for the wireless networks.
Connection Tracking
Regarding connection tracking there is conntrack running with support for 20480 connections and 4096 buckets for the hash-table.
The other settings for conntrack appear to be reasonable at first glance:
root@NR7101:/usr/sbin# sysctl -a | grep net.netfilter.nf_conntrack
sysctl: error reading key 'net.ipv4.route.flush': Permission denied
sysctl: error reading key 'net.ipv6.route.flush': Permission denied
net.netfilter.nf_conntrack_acct = 0
net.netfilter.nf_conntrack_buckets = 4096
net.netfilter.nf_conntrack_checksum = 1
net.netfilter.nf_conntrack_count = 17
net.netfilter.nf_conntrack_expect_max = 60
net.netfilter.nf_conntrack_frag6_high_thresh = 4194304
net.netfilter.nf_conntrack_frag6_low_thresh = 3145728
net.netfilter.nf_conntrack_frag6_timeout = 60
net.netfilter.nf_conntrack_generic_timeout = 600
net.netfilter.nf_conntrack_helper = 1
net.netfilter.nf_conntrack_icmp_timeout = 30
net.netfilter.nf_conntrack_icmpv6_timeout = 30
net.netfilter.nf_conntrack_log_invalid = 0
net.netfilter.nf_conntrack_max = 20480
net.netfilter.nf_conntrack_tcp_be_liberal = 0
net.netfilter.nf_conntrack_tcp_loose = 1
net.netfilter.nf_conntrack_tcp_max_retrans = 3
net.netfilter.nf_conntrack_tcp_timeout_close = 10
net.netfilter.nf_conntrack_tcp_timeout_close_wait = 60
net.netfilter.nf_conntrack_tcp_timeout_established = 3600
net.netfilter.nf_conntrack_tcp_timeout_fin_wait = 120
net.netfilter.nf_conntrack_tcp_timeout_last_ack = 30
net.netfilter.nf_conntrack_tcp_timeout_max_retrans = 300
net.netfilter.nf_conntrack_tcp_timeout_syn_recv = 60
net.netfilter.nf_conntrack_tcp_timeout_syn_sent = 120
net.netfilter.nf_conntrack_tcp_timeout_time_wait = 120
net.netfilter.nf_conntrack_tcp_timeout_unacknowledged = 300
net.netfilter.nf_conntrack_udp_timeout = 30
net.netfilter.nf_conntrack_udp_timeout_stream = 180
The conntrack tool is also available.
conntrack -L lists the tracked sessions while conntrack -C returns the
amount of tracked sessions.
IPTables
The router is running iptables as a firewall. The firewall is very lengthy, a dump of the rules can be found in a GitHub repository.
In general there are a lot of tables that are empty by default. In IP-Passthrough mode the FORWARD chain simply accepts everything. The INPUT chain allows the protocols defined for remote management and everything that has a RELATED/ESTABLISHED state.
Benchmarks
Bandwidth-Test
We will start with simple bandwidth test to get an estimate for the maximum bandwidth available.
For this we are running iperf3 for 60 seconds, once with the client as sender, receiver and one in bidirectional mode.
We repeat the test with 10 parallel sessions to check, that that we are not limited by a single flow.
The throughput depends a lot on the signal strength and the general usage of the cell we are in. During daytime the tests were in the range of 60-120Mbit/s download speed, however during the early morning hours on a Sunday we were able to achieve the 350Mbit/s that are advertised by the ISP in the area we tested in.
During this test the CPU utilization never got beyond 10%.
new-sessions per second test
To test how many new sessions the device can handle we generate them via trafgen and this package description:
{
# --- ethernet header ---
eth(sa=aa:bb:cc:dd:ee:ff, da=gg:hh:ii:jj:kk:ll)
# --- ip header ---
ipv4(id=drnd(), ttl=64, sa=A.B.C.D, da=E.F.G.H)
# --- UDP header ---
udp(sport=48054, dport=dinc(10000, 50000), csum=0)
# payload
'A', fill(0x41, 11),
}
The MAC and IP addresses have to be adjusted accordingly. This generates a new session by increasing the UDP destination port. The test is then executed with the following command.
trafgen -o enp0s31f6: -i packet.dsc -P 4 -b 300pps
In this case we are testing with 300 packets (which is equivalent to 300 sessions in this case).
Somewhere between 250 and 300 new sessions per second the Zyxel device starts sending Pause-frames and has one of the four cores completely utilized with interrupt handling. This is due to all interrupts being handled on one core.
root@NR7101:~# cat /proc/interrupts
CPU0 CPU1 CPU2 CPU3
3: 0 2115968 0 0 MIPS GIC eth2
Since irqbalance is not installed we can't easily redistribute these interrupts.
Reducing the amount of allowed conntrack sessions
When we reduce the amount of conntrack sessions to something very low we can test what happens when the conntrack table is full.
We set it to 80 with echo "80" > /proc/sys/net/netfilter/nf_conntrack_max.
Then we ran a iperf test with 100 sessions in parallel.
iperf could not open all of these sessions, because the conntrack session table
was full and the router started dropping packets and informed us in dmesg:
...
[14008.628000] nf_conntrack: table full, dropping packet
[14009.636000] nf_conntrack: table full, dropping packet
[14011.904000] nf_conntrack: table full, dropping packet
[14012.916000] nf_conntrack: table full, dropping packet
...
There are now stateful matches in the iptables rules for the path these packets take, but they are dropped regardless.
disabling conntrack for sessions that don't go through the device
We tried to disable connection tracking for all flows that only go through the
device, however the firmware that is running on the device does not allow for
that. The NOTRACK target and the --notrack option for the CT
target are unknown to the device:
root@NR7101:/# iptables -t raw -A PREROUTING -d 1.2.3.4 -j CT --notrack
iptables v1.4.16.3: unknown option "--notrack"
Try `iptables -h' or 'iptables --help' for more information.
root@NR7101:/# iptables -t raw -A PREROUTING -d 1.2.3.4 -j NOTRACK
iptables v1.4.16.3: Couldn't find target `NOTRACK'
Try `iptables -h' or 'iptables --help' for more information.
So disabling connection tracking is not easily possible.
Increasing the amount of conntrack sessions
We can adjust the maximum amount of conntrack sessions and the conntrack bucket size, if we run into the packet-drop problem.
echo "40960" > /proc/sys/net/netfilter/nf_conntrack_max
echo "8192" > /sys/module/nf_conntrack/parameters/hashsize
For a detailed discussion of those values take a look this Conntrack Parameter Tuning wiki page.
Conclusion
The NR7101 has some limitations regarding the amount of sessions it can handle.
There is no direct solution available, however increasing the nf_conntrack_max
can help a bit.
There is no easy workaround for the limited amount of new sessions per second.
An other option could be to use the OpenWrt firmware instead.
Remarks regarding the NR7102
The NR7102 comes from the same series of devices as the NR7101. From the outside and the Web UI this device looks very similar to the NR7101. However the method to gain a root password does not work here. So we can't take a deeper look into this device.
Building a simple Linux multipath router
2022-05-03
I am occasionally running LAN parties. The available internet bandwidth is often an issue. I wanted a simple way to balance traffic over multiple internet uplinks. It is assumed that there will be NAT on or after the egress interface of the router.
This first version tries to be simple, while not being optimal in all cases.
The basic feature we will be using is multipath routing. Instead of a simple default route our router will have a default route with multiple nexthops. This can be added via iproute2:
ip route add 0.0.0.0/0 \
nexthop via 172.21.0.1 dev bond0.300 weight 3 \
nexthop via 172.21.101.1 dev eno1 weight 1
This route will balance the traffic to the nexthops 172.21.0.1 and
172.21.101.1 over the specified interfaces.
The weight setting will balance the flows (statistically) 3 to 1
between the links.
You can adjust that according to your available bandwidth.
You also might want to check, that there is no other default route with a lower metric, because that will be preferred.
L4 Hashing
By default the load balancing is only done on L3 (IP) headers. A hash is calculated over these fields and that is then used to assign the flow to a nexthop. So given a big enough number of flows you should see a flow distribution according to your weights. To use the L4 headers (which will make it possible to balance flows of the same client over different uplinks) we have to set the sysctl
net.ipv4.fib_multipath_hash_policy = 1
Caveats
There are some issues with this setup:
- It is not tested in production yet.
- There might be issues with protocols that use multiple ports in parallel (e.g. ftp) or services that need to track users by IP address. This might be "solved" by sticking to L3 header hashing only.
- This setup in this naive form does not consider link latency and special traffic classification
- This does not handle traffic shaping. If you want to rate limit the traffic, you have to do this via
tc,nftor whatever you prefer. - In the case that you are not running NAT but have a public address space that is reachable via all of your uplinks you can only control the way packets are leaving your network. The ingress way is out of your control.
- Keep in mind that different flows might cause different amounts of traffic. If you have 100 flows and a 1:1 split, then you will see ~50 flows per nexthop. If you are unlucky the 50 flows for one nexthop might need a lot of traffic and fill up that link while the other 50 are not enough to fill the other link. Although this scenario is rather unlikely.
Testing the setup
To test the setup you have to send traffic from an address that is not on the transit networks to your nexthops, because otherwise the route selection algorithm might influence the route decision
You can use mtr -I $iface 9.9.9.9 to check which nexthop you get.
Just select a appropriate interface or use a second computer behind the router.
In the later case you can skip the -I $iface parameter.
When you use several different destination addresses you should see the different
nexthops you specified.
Alternatively ip route get $target from $address should return you different
next hops for different targets.
References
- https://codecave.cc/multipath-routing-in-linux-part-2.html
- https://sysctl-explorer.net/net/ipv4/fib_multipath_hash_policy/
- https://manpages.debian.org/jessie/iproute2/ip-route.8.en.html
Booting Cisco 3560E switches with IOS 15.2 does not work
2021-09-01
TL;DR: You can not boot IOS 15.2 from the 3560X switches on 3560E switches.
The why and what happens if you try it
I have a couple of 3560E switches.
Sadly they only run IOS 15.0.
I wanted to have IPv4 address families over OSPFv3.
This is not supported in IOS 15.0.
But it is in IOS 15.2.
And the IOS 15.2 image for the successor model to the 3560E,
the 3560X, is called c3560e-universalk9-mz.152-4.E10.bin.
And the IOS 15.0 firmware for the 3560X switches is the same file as for the
3560.
So I tried to boot the 15.2(4)-E10 image.
The switch itself boots the image but hits a malloc error during the boot
process, crashes and reboots.
So no OSPFv3 with IPv4 address family on those switches.
Here is the output of the boot process:
<...snip...>
POST: Thermal, Fan Tests : Begin
POST: Thermal, Fan Tests : End, Status Passed
POST: PortASIC Port Loopback Tests : Begin
POST: PortASIC Port Loopback Tests : End, Status Passed
POST: EMAC Loopback Tests : Begin
POST: EMAC Loopback Tests : End, Status Passed
Waiting for Port download...Complete
SYSTEM INIT: INSUFFICIENT MEMORY TO BOOT THE IMAGE!
%Software-forced reload
00:01:01 UTC Mon Jan 2 2006: Unexpected exception to CPUvector 2000, PC = 36828B0
-Traceback= 0x36828B0z 0x2AFD98Cz 0x2B05F5Cz 0x3678A24z 0x367DF60z 0x2B2A9E0z 0x31D2AE0z 0x3118FDCz 0x3206400z 0x3209A2Cz 0x2AE5D30z 0x2AE5EFCz 0x2AE604Cz 0x6D921Cz 0x6D9454z 0x3683BA0z
Writing crashinfo to flash:/crashinfo_ext/crashinfo_ext_4
=== Flushing messages (00:01:03 UTC Mon Jan 2 2006) ===
Buffered messages:
Queued messages:
*Jan 2 00:01:03.929: %SYS-3-LOGGER_FLUSHING: System pausing to ensure console debugging output.
*Mar 1 00:00:07.012: Read env variable - LICENSE_BOOT_LEVEL =
*Jan 2 00:00:03.456: %IOS_LICENSE_IMAGE_APPLICATION-6-LICENSE_LEVEL: Module name = c3560e Next reboot level = ipservices and License = ipservices
*Jan 2 00:01:01.329: %SYS-2-MALLOCFAIL: Memory allocation of 60000 bytes failed from 0x3678A20, alignment 0 <<< This is the relevant part.
Pool: Processor Free: 38104 Cause: Not enough free memory
Alternate Pool: None Free: 0 Cause: No Alternate pool
-Process= "Init", ipl= 0, pid= 3
-Traceback= 6C9738z 2AFD8F8z 2B05F5Cz 3678A24z 367DF60z 2B2A9E0z 31D2AE0z 3118FDCz 3206400z 3209A2Cz 2AE5D30z 2AE5EFCz 2AE604Cz 6D921Cz 6D9454z 3683BA0z
Cisco IOS Software, C3560E Software (C3560E-UNIVERSALK9-M), Version 15.2(4)E10, RELEASE SOFTWARE (fc2)
Technical Support: http://www.cisco.com/techsupport
Copyright (c) 1986-2020 by Cisco Systems, Inc.
Compiled Tue 31-Mar-20 21:44 by prod_rel_team
Debug Exception (Could be NULL pointer dereference) Exception (0x2000)!
SRR0 = 0x031BB534 SRR1 = 0x00029230 SRR2 = 0x036828B0 SRR3 = 0x00029230
ESR = 0x00000000 DEAR = 0x00000000 TSR = 0x84000000 DBSR = 0x10000000
CPU Register Context:
Vector = 0x00002000 PC = 0x036828B0 MSR = 0x00029230 CR = 0x35000053
LR = 0x0368284C CTR = 0x006B4068 XER = 0xE0000075
R0 = 0x0368284C R1 = 0x06357288 R2 = 0x00000000 R3 = 0x04F897A8
R4 = 0x00000000 R5 = 0x00000000 R6 = 0x06357258 R7 = 0x05850000
R8 = 0x00029230 R9 = 0x05850000 R10 = 0x00008000 R11 = 0x00000000
R12 = 0x35000059 R13 = 0x079817A8 R14 = 0x053AFDD8 R15 = 0x00000000
R16 = 0x038B2550 R17 = 0x00000004 R18 = 0x00000020 R19 = 0x05850000
R20 = 0x00000000 R21 = 0x00000000 R22 = 0x0000EA60 R23 = 0x00000000
R24 = 0x00000000 R25 = 0x053AFDD8 R26 = 0x03678A20 R27 = 0x0000EA60
R28 = 0x00000000 R29 = 0x05EE80C0 R30 = 0x05BA0978 R31 = 0x00000000
Stack trace:
PC = 0x036828B0, SP = 0x06357288
Frame 00: SP = 0x06357298 PC = 0x0368284C
Frame 01: SP = 0x063572C8 PC = 0x02AFD98C
Frame 02: SP = 0x06357360 PC = 0x02B05F5C
Frame 03: SP = 0x06357378 PC = 0x03678A24
Frame 04: SP = 0x06357390 PC = 0x0367DF60
Frame 05: SP = 0x063573C0 PC = 0x02B2A9E0
Frame 06: SP = 0x063573E8 PC = 0x031D2AE0
Frame 07: SP = 0x06357400 PC = 0x03118FDC
Frame 08: SP = 0x06357418 PC = 0x03206400
Frame 09: SP = 0x06357458 PC = 0x03209A2C
Frame 10: SP = 0x06357468 PC = 0x02AE5D30
Frame 11: SP = 0x06357488 PC = 0x02AE5EFC
Frame 12: SP = 0x063574A0 PC = 0x02AE604C
Frame 13: SP = 0x063574D0 PC = 0x006D921C
Frame 14: SP = 0x063575D8 PC = 0x006D9454
Frame 15: SP = 0x063575E0 PC = 0x03683BA0
<...switch reboots...>
The other interesting problem is now: How to reset the switch? Normaly the switch would try the next image on disk if the first one fails, but this image works "good enough" for that mechanic not to kick in. This means that the switch is stuck in an infinite boot loop.
Resetting the switch to the old image
Disconnect the power, connect to the console port, press and hold the Mode
button. Then plug the power cord back in.
After 10-20 seconds release the Mode button.
After a short time the switch: prompt should appear and you are in the
bootloader.
To boot the old image you have to initialize the filesystem (flash_init),
find the image with dir flash:
and delete it with delete flash:/c3560e-universalk9-mz.152-4.E10.bin.
After that boot the switch with boot.
The switch tries to boot the image that is in the config file, fails and tries
the first available image on the device which is probably your old working
image.
If no working image is on the flash have fun with xmodem or tftp.
Using driver version 1 for media type 2
Base ethernet MAC Address: 08:1f:f3:39:8c:80
Xmodem file system is available.
The password-recovery mechanism is enabled.
The system has been interrupted prior to initializing the
flash filesystem. The following commands will initialize
the flash filesystem, and finish loading the operating
system software:
flash_init
boot
switch: ?
? -- Present list of available commands
boot -- Load and boot an executable image
cat -- Concatenate (type) file(s)
copy -- Copy a file
delete -- Delete file(s)
dir -- List files in directories
flash_init -- Initialize flash filesystem(s)
format -- Format a filesystem
fsck -- Check filesystem consistency
help -- Present list of available commands
memory -- Present memory heap utilization information
mkdir -- Create dir(s)
more -- Concatenate (display) file(s)
rename -- Rename a file
reset -- Reset the system
rmdir -- Delete empty dir(s)
set -- Set or display environment variables
set_bs -- Set attributes on a boot sector filesystem
set_param -- Set system parameters in flash
sleep -- Pause (sleep) for a specified number of seconds
type -- Concatenate (type) file(s)
unset -- Unset one or more environment variables
version -- Display boot loader version
switch: flash_init
Initializing Flash...
mifs[2]: 10 files, 1 directories
mifs[2]: Total bytes : 2097152
mifs[2]: Bytes used : 614400
mifs[2]: Bytes available : 1482752
mifs[2]: mifs fsck took 2 seconds.
mifs[3]: 3 files, 1 directories
mifs[3]: Total bytes : 4194304
mifs[3]: Bytes used : 949248
mifs[3]: Bytes available : 3245056
mifs[3]: mifs fsck took 2 seconds.
mifs[4]: 5 files, 1 directories
mifs[4]: Total bytes : 524288
mifs[4]: Bytes used : 9216
mifs[4]: Bytes available : 515072
mifs[4]: mifs fsck took 0 seconds.
mifs[5]: 5 files, 1 directories
mifs[5]: Total bytes : 524288
mifs[5]: Bytes used : 9216
mifs[5]: Bytes available : 515072
mifs[5]: mifs fsck took 1 seconds.
-- MORE --
mifs[6]: 15 files, 3 directories
mifs[6]: Total bytes : 57671680
mifs[6]: Bytes used : 49069056
mifs[6]: Bytes available : 8602624
mifs[6]: mifs fsck took 26 seconds.
...done Initializing Flash.
switch: dir
List of filesystems currently registered:
bs[0]: (read-only)
flash[6]: (read-write)
xmodem[7]: (read-only)
null[8]: (read-write)
switch: dir flash:
Directory of flash:/
2 -rwx 20310016 <date> c3560e-universalk9-mz.150-2.SE11.bin
3 drwx 512 <date> crashinfo_ext
8 -rwx 1560 <date> express_setup.debug
9 -rwx 916 <date> vlan.dat
10 -rwx 64 <date> ztp.py
11 -rwx 26771456 <date> c3560e-universalk9-mz.152-4.E10.bin
12 -rwx 1920 <date> private-config.text
13 -rwx 5144 <date> multiple-fs
14 -rwx 6223 <date> config.text
15 drwx 512 <date> crashinfo
8602624 bytes available (49069056 bytes used)
switch: delete flash:c3560e-universalk9-mz.152-4.E10.bin
Are you sure you want to delete "flash:c3560e-universalk9-mz.152-4.E10.bin" (y/n)?y
File "flash:c3560e-universalk9-mz.152-4.E10.bin" deleted
switch: boot
Loading "flash:c3560e-universalk9-mz.152-4.E10.bin"...flash:c3560e-universalk9-mz.152-4.E10.bin: no such file or directory
Error loading "flash:c3560e-universalk9-mz.152-4.E10.bin"
Interrupt within 5 seconds to abort boot process.
Loading "flash:/c3560e-universalk9-mz.150-2.SE11.bin"...@@@@@@@@@@@@@@@<... switch booting image as usual ...>
Compressing IPv6 Addresses with Regular Expressions
2021-03-06
This post was lying around for too long, time to finish it and get it off my todo list.
The Goal
Convert from a full IPv6 address like
2001:0db8:0000:0000:0000:0023:4200:0123
to a compressed one like
2001:db8::23:4200:123 with a regular expression.
Why? Because I can. And because some prometheus exporters only give you the
uncompressed addresses.
Details regarding IPv6 address compression can be found in RFC 5952 Section 4.
Preprocessing
The first step is to get from the full form to a form where the leading zeros are removed/reduced to just a single zero per block.
This could be done like this:
^0{0,3}(.*:)0{0,3}(.*:)0{0,3}(.*:)0{0,3}(.*:)0{0,3}(.*:)0{0,3}(.*:)0{0,3}(.*:)0{0,3}(.*)$
and $1$2$3$4$5$6$7$8 as a replacement string.
This results in 2001:db8:0:0:0:23:4200:123
The Common Case
Now the funny part begins. Basically we have to find the first longest sequence
of zero-blocks that is longer than 1 block. If we make a group with everything to
the left and right of that (including the : ) and combine the 2
groups we get the result. There are some corner cases, those will be handled
later.
To find a sequence of length N we can build a very simple expression like
0:0:< in total N zeros >:0:0
Everything to the left of that must have less N consecutive zero blocks.
A expression to match that could be:
((0:){0,$N-1}[1-9a-f][0-9a-f]{0,3}:)*
Everything to the right of the zero block sequence can have at most N
consecutive zero blocks. The expression for that looks like this.
(:[1-9a-f][0-9a-f]{0,3}(:0){0,$N})*
Combined they result in this expression:
(((0:){0,$N-1}[1-9a-f][0-9a-f]{0,3}:)*)0:0:< in total N zeros >:0:0((:[1-9a-f][0-9a-f]{0,3}(:0){0,$N})*)
Combining the first and fourth group of that expression results in the
compressed representation of the address, if the longest zero block sequence is
N blocks long. We can build the expression for all possible block lengths.
The Corner Cases
As mentioned earlier there are several corner cases.
Compression at the left or right side
If the longest sequence is at the left or right end
(e.g. 0:0:0:0:0:0:1:2 and 2:1:0:0:0:0:0:0) then we need a
special expression. For the left side it looks like this:
0(:)0:< N-1 times 0 in total >:0:0((:[1-9a-f][0-9a-f]{0,3}(:0){0,$N})*)
This solves 2 problems:
- The group that would be on the left side with the expression for the common case needs to be removed, because there is nothing to match there.
- we have to find a
:to build the::in the compressed representation. This is done by taking one from theNzero blocks of the longest sequence.
the right side is constructed the same way.
Compressing 7 consecutive zero blocks
When there are 7 consecutive zero blocks then the compression will happen at either the left or right side, because there is only one non zero block left. for the 7 only the two expressions for the sides are needed, not the common one.
Compressing 8 zero blocks
All the other expressions don't work for the one case of 8 consecutive zeros.
But we have to get 2 : for the :: from somewhere.
This could look like this:
0(:)0(:)0:0:0:0:0:0
Combining it all
In total we get 3 expressions each for 2, 3, 4, 5 and 6 consecutive zero blocks, 2 for the 7 consecutive zero blocks and 1 for the 8 zero blocks.
Those 18 expressions can be combined like this:
^(($EXPR1)|($EXPR2)|...)$
Building all of this by hand is shitty and annoying. Here is some code to do it.
zero = "0"
non_zero = "[1-9a-f]"
all_chars = "[0-9a-f]"
non_zero_chunk = f"{non_zero}{all_chars}{{0,3}}"
def max_n_zero_block_left(n: int) -> str:
return f"((({ zero }:){{0,{n}}}{ non_zero_chunk }:)*)"
def max_n_zero_block_right(n: int) -> str:
return f"((:{ non_zero_chunk }(:{ zero }){{0,{n}}})*)"
def n_length_zero_block(n: int) -> str:
return ":".join(zero*n)
left_zero_prefix = f"0(:)"
right_zero_suffix = f"(:)0"
patterns = list()
replacement_positions = list()
next_pattern_group_start = 1
for n in range(7,1,-1):
# special case for the longest continuos zero string at the left
pattern = f"({ left_zero_prefix }{ n_length_zero_block(n - 1) }({ max_n_zero_block_right(n) }))"
patterns.append(pattern)
replacement_positions.append(next_pattern_group_start + 2)
replacement_positions.append(next_pattern_group_start + 3)
next_pattern_group_start += 6
# special case for ending with 0
pattern = f"(({ max_n_zero_block_left(n-1) }){ n_length_zero_block(n - 1) }{ right_zero_suffix })"
patterns.append(pattern)
replacement_positions.append(next_pattern_group_start + 2)
replacement_positions.append(next_pattern_group_start + 6)
next_pattern_group_start += 6
if n == 7:
continue # the regular case does not exist for n=7
# regular case
pattern = f"(({ max_n_zero_block_left(n-1) }){ n_length_zero_block(n) }({ max_n_zero_block_right(n) }))"
patterns.append(pattern)
replacement_positions.append(next_pattern_group_start + 2)
replacement_positions.append(next_pattern_group_start + 6)
next_pattern_group_start += 9
patterns.append("(0(:)0(:)0:0:0:0:0:0)")
replacement_positions.append(next_pattern_group_start + 2)
replacement_positions.append(next_pattern_group_start + 3)
all_patterns = "|".join(patterns)
all_patterns = "^(" + all_patterns + ")$"
print("Expression:")
print(all_patterns)
replacement = "".join(f"${{{i}}}" for i in replacement_positions)
print("Replacement:")
print(replacement)
And the output of the script:
Expression:
^((0(:)0:0:0:0:0:0(((:[1-9a-f][0-9a-f]{0,3}(:0){0,7})*)))|(((((0:){0,6}[1-9a-f][0-9a-f]{0,3}:)*))0:0:0:0:0:0(:)0)|(0(:)0:0:0:0:0(((:[1-9a-f][0-9a-f]{0,3}(:0){0,6})*)))|(((((0:){0,5}[1-9a-f][0-9a-f]{0,3}:)*))0:0:0:0:0(:)0)|(((((0:){0,5}[1-9a-f][0-9a-f]{0,3}:)*))0:0:0:0:0:0(((:[1-9a-f][0-9a-f]{0,3}(:0){0,6})*)))|(0(:)0:0:0:0(((:[1-9a-f][0-9a-f]{0,3}(:0){0,5})*)))|(((((0:){0,4}[1-9a-f][0-9a-f]{0,3}:)*))0:0:0:0(:)0)|(((((0:){0,4}[1-9a-f][0-9a-f]{0,3}:)*))0:0:0:0:0(((:[1-9a-f][0-9a-f]{0,3}(:0){0,5})*)))|(0(:)0:0:0(((:[1-9a-f][0-9a-f]{0,3}(:0){0,4})*)))|(((((0:){0,3}[1-9a-f][0-9a-f]{0,3}:)*))0:0:0(:)0)|(((((0:){0,3}[1-9a-f][0-9a-f]{0,3}:)*))0:0:0:0(((:[1-9a-f][0-9a-f]{0,3}(:0){0,4})*)))|(0(:)0:0(((:[1-9a-f][0-9a-f]{0,3}(:0){0,3})*)))|(((((0:){0,2}[1-9a-f][0-9a-f]{0,3}:)*))0:0(:)0)|(((((0:){0,2}[1-9a-f][0-9a-f]{0,3}:)*))0:0:0(((:[1-9a-f][0-9a-f]{0,3}(:0){0,3})*)))|(0(:)0(((:[1-9a-f][0-9a-f]{0,3}(:0){0,2})*)))|(((((0:){0,1}[1-9a-f][0-9a-f]{0,3}:)*))0(:)0)|(((((0:){0,1}[1-9a-f][0-9a-f]{0,3}:)*))0:0(((:[1-9a-f][0-9a-f]{0,3}(:0){0,2})*)))|(0(:)0(:)0:0:0:0:0:0))$
Replacement:
${3}${4}${9}${13}${15}${16}${21}${25}${27}${31}${36}${37}${42}${46}${48}${52}${57}${58}${63}${67}${69}${73}${78}${79}${84}${88}${90}${94}${99}${100}${105}${109}${111}${115}${120}${121}
Please keep in mind that I am just an idiot on the internet, don't use this expression to burn your production environment down.
Interesting Observations of IOS(-XE) ACL CLI and Command Syntax
2020-11-26
My initial contact for the things shown in this article comes from trying to parse and generate ACLs. Many of the things here may not bother you, if you are a pure CLI user and are not generating configs. This article does not claim to be the ultimate source for all the weird details of ACL syntax behaviour. This is based on my experience which primarily comes from IOS 15.7, IOS-XE 03.16, IOS-XE 16.09 and 16.12. IOS-XE 16.12 changed a lot in regards to sequence numbers. So there will be several sections that will be divided into a pre IOS-XE 16.12 part and a post IOS-XE 16.12 part. the regular IOS can be considered a part of the pre IOS-XE 16.12 sections, because I have not found differences between those.
General things
An Access Control List is a series of entries. Each entry matches some parts of a the packet headers. Each entry is either a remark or a permit or deny action. (I will ignore reflexive ACLs and the like here.)
Sequence Numbers
Each entry in an ACL has a sequence number. By default the first entry starts at 10 and every further entry has a number that is 10 higher.
When modifying entries you can specify a sequence number at which position you want to add something. So if you want to insert something between entry 10 and 20 you could choose a unused number between 10 and 20, e.g. 15.
Resequencing
But what happens if you want to insert between two entries where there is no
free sequence number? For Legacy IP ACLs you can do a
ip access-list <type> <name> resequence which renumbers the entries so that
each entry is now 10 numbers apart again.
But that is not implemented for IPv6... A workaround is to recreate the ACL. But that is annoying.
IPv4
Pre IOS-XE 16.12
On IOS and IOS-XE the IPv4 sequence numbers are not a part the config.
This means that you have to do show ip access-list ...
to see the sequence numbers.
They are generated at runtime.
This also means that the sequence numbers change after a reboot.
Post IOS-XE 16.12
Sequence numbers are now a part of the configuration. The implications will be discussed later.
IPv6
Pre IOS-XE 16.12
IPv6 sequence numbers can be a part of the config. They are shown on a per entry basis if the sequence number is not exactly 10 bigger than the previous one.
If you enter the commands:
ipv6 access-list test
sequence 10 permit ipv6 host 2001:db8::1 any
sequence 15 permit ipv6 host 2001:db8::2 any
sequence 20 permit ipv6 host 2001:db8::3 any
sequence 25 permit ipv6 host 2001:db8::4 any
sequence 35 permit ipv6 host 2001:db8::5 any
sequence 40 permit ipv6 host 2001:db8::6 any
Then the ACL in the config is this:
ipv6 access-list test
permit ipv6 host 2001:DB8::1 any
sequence 15 permit ipv6 host 2001:DB8::2 any
sequence 20 permit ipv6 host 2001:DB8::3 any
sequence 25 permit ipv6 host 2001:DB8::4 any
permit ipv6 host 2001:DB8::5 any
sequence 40 permit ipv6 host 2001:DB8::6 any
The 2001:db8::2, 2001:db8::3 and 2001:db8::4 have numbers because their
distance to the sequence number of the previous entry is 5.
2001:db8::5 has no number because the distance is 10, and 2001:db8::6 has a
distance of 5 and therefore has a sequence number.
The show ipv6 access-list test command shows you all sequence numbers,
but at the end of the entry, not at the beginning like your config file does it.
IPv6 access list test
permit ipv6 host 2001:DB8::1 any sequence 10
permit ipv6 host 2001:DB8::2 any sequence 15
permit ipv6 host 2001:DB8::3 any sequence 20
permit ipv6 host 2001:DB8::4 any sequence 25
permit ipv6 host 2001:DB8::5 any sequence 35
permit ipv6 host 2001:DB8::6 any sequence 40
Post IOS-XE 16.12
In IOS-XE 16.12 the sequence numbers are always shown in the config. So there is at least one point where IOS got more consistent.
ipv6 access-list test
sequence 10 permit ipv6 host 2001:DB8::1 any
sequence 15 permit ipv6 host 2001:DB8::2 any
sequence 20 permit ipv6 host 2001:DB8::3 any
sequence 25 permit ipv6 host 2001:DB8::4 any
sequence 35 permit ipv6 host 2001:DB8::5 any
sequence 40 permit ipv6 host 2001:DB8::6 any
But sadly the output of the show ipv6 access-list command still puts the
sequence number at the end of the entries.
IPv4 Remarks
IPv4 ACL Remarks do not have their own sequence numbers.
Pre IOS-XE 16.12
This means inserting remarks in IPv4 ACLs at a specific position does not work.
Only permit and deny are allowed.
asr920(config-ext-nacl)#42 ?
deny Specify packets to reject
permit Specify packets to forward
If you want to add a remark somewhere in the middle you have to delete the whole ACL, and insert the remark at the correct position while recreating the ACL.
But if you want to insert a new entry with a remark you can work your way around this issue. First you insert a remark without a sequence number and insert an entry with a sequence number and that remark will end up at the same position as the other entry.
ip access-list extended abcd
10 permit ip host 10.0.0.0 any
20 permit ip host 10.0.0.1 any
remark test
15 permit ip host 10.0.0.2 any
results in
ip access-list extended abcd
permit ip host 10.0.0.0 any
remark test
permit ip host 10.0.0.2 any
permit ip host 10.0.0.1 any
Post IOS-XE 16.12
In IOS-XE 16.12 every entry got a sequence number. But as mentioned earlier, IPv4 remarks did not have sequence numbers. So Cisco "solved" that. An ACL now looks like this in the config:
ip access-list extended remark-seq-numbers
10 remark foo
10 permit ip host 10.0.0.0 any
20 remark bar
20 permit ip host 10.0.0.42 any
Also inserting remarks at a specific sequence number works now (to some degree).
If you enter 15 remark test for the ACL above you get this:
ip access-list extended remark-seq-numbers
10 remark foo
10 permit ip host 10.0.0.0 any
20 remark bar
20 remark asdf
20 permit ip host 10.0.0.42 any
15 remark test
Our remark is now at the end, where it does not belong. This change in IOS-XE 16.12 does result in sequence numbers appearing multiple times and being out of order.
Reusing the same sequence number
When you want to replace an entry in an IPv6 ACL with an other one you can just use the same sequence number and the entry will be replaced.
If you try that with an IPv4 permit/deny entry you get this response:
% Duplicate sequence number
%Failed to add ace to access-list
(yes, the space after the % in the first line and the lack thereof in the
second is not a copy+paste error.)
However if you do this in IOS-XE 16.12 with a remark line it works just fine and it replaces the remark.
Singular/Plural in the ACL show commands
While the config commands for ACLs are ip[v6] access-list the show-commands are
show ip access-lists with a s at the end and show ipv6 access-list without
a s at the end.
c1111-lab#show ip access-lists
Standard IP access list 2
...
c1111-lab#show ipv6 access-list
IPv6 access list test
...
c1111-lab#show ipv6 access-lists
^
% Invalid input detected at '^' marker.
ACL naming: numbers vs names
There is not only the difference between standard and extended ACLs, there is also a difference between ACLs with a name and ACLs with a number. Which numbers can be given to an ACL depends on their type.
asr920(config)#access-list ?
<1-99> IP standard access list
<100-199> IP extended access list
<1300-1999> IP standard access list (expanded range)
<2000-2699> IP extended access list (expanded range)
<2700-2799> MPLS access list
<snip>
To make things more complicated the numbers for standard and extended ACLs each have 2 seperate ranges.
A little tip at this point: do not use numbered ACLs. Use ACLs with names,
because you can give them a name that hopefully tells you and others what this
ACL is for. Or can you remember what ACL 42 was for? and where it is used?
(good luck with sh run | incl 42 for large configs)
Standard vs Extended Numbered ACL Config format
Pre IOS-XE 16.12
If you use an extended ACL with a number (please don't) you probably enter
ip access-list extended 101
permit ip host 10.0.0.0 any
and that is exactly what will end up in your config. However if you want to use a standard ACL with a number (pls dont) you enter
ip access-list standard 1
permit host 10.0.0.0
And you will end up with this in your config:
access-list 1 permit 10.0.0.0
post IOS-XE 16.12
This format is no longer used in IOS XE 16.12, it has been changed to the same format as named ACLs are using and it looks like this:
ip access-list standard 1
10 permit 10.0.0.0
This is nice, because it is less inconsistent. But unless you have absolutly no legacy gear you have to support it anyways.
Remarks
Remarks are very handy when trying to understand lengthy ACLs (lengthy in my case
sometimes means hundreds of lines, but others might laught at that).
Sadly IOS does not show remarks with show ip access-list, for those you have
to take a look into your config.
Interface-ACLs that do not exist
If you delete an ACL that is configured on an interface, the config line is not deleted from the interface. But the interface now accepts all traffic.
asr920(config)#ip access-list extended delete-test
asr920(config-ext-nacl)#deny ip any any
asr920(config-ext-nacl)#do sh run int Gi0/0/0
interface GigabitEthernet0/0/0
ip address dhcp
ip access-group delete-test in
negotiation auto
end
asr920(config-ext-nacl)#do sh ip access-list delete-test
Extended IP access list delete-test
10 deny ip any any
asr920(config-ext-nacl)#do ping 10.0.0.1
Type escape sequence to abort.
Sending 5, 100-byte ICMP Echos to 10.0.0.1, timeout is 2 seconds:
.....
Success rate is 0 percent (0/5)
asr920(config-ext-nacl)#exit
asr920(config)#no ip access-list extended delete-test
asr920(config)#do sh ip access-list delete-test
asr920(config)#do sh run int Gi0/0/0
interface GigabitEthernet0/0/0
ip address dhcp
ip access-group delete-test in
negotiation auto
end
asr920(config)#do ping 10.0.0.1
Type escape sequence to abort.
Sending 5, 100-byte ICMP Echos to 10.0.0.1, timeout is 2 seconds:
!!!!!
Success rate is 100 percent (5/5), round-trip min/avg/max = 1/1/4 ms
IPv4 ACLs that only consist of remarks
But what if the ACL exists but there is no action statement in an ACL at all? We can build such an ACL that is only a remark. The ACL shows up in the config, but the default deny does not deny all traffic. But when we add an action the implicit deny suddenly works.
asr920(config)#ip access-list extended noentry
asr920(config-ext-nacl)#remark test1
asr920(config)#do sh run | section ip access-list extended noentry
ip access-list extended noentry
remark test1
asr920(config-std-nacl)#in Gi0/0/0
asr920(config-if)#ip access-group noentry in
asr920(config-if)#do ping 10.0.0.42
Type escape sequence to abort.
Sending 5, 100-byte ICMP Echos to 10.0.0.42, timeout is 2 seconds:
!!!!!
Success rate is 100 percent (5/5), round-trip min/avg/max = 1/2/4 ms
asr920(config-if)#exit
asr920(config)#ip access-list extended noentry
asr920(config-ext-nacl)#permit ip host 192.168.0.0 any
asr920(config-ext-nacl)#do ping 10.0.0.42
Type escape sequence to abort.
Sending 5, 100-byte ICMP Echos to 10.0.0.42, timeout is 2 seconds:
.....
Success rate is 0 percent (0/5)
Default settings for config sections that can have an ACL
Things like SSH, NTP, SNMP, NETCONF, ... may (and probably should) be secured by ACLs. But by default they are not protected and answer to everything. This means you want to have an ACL for all of them. For IPv4 and IPv6. If you add the first IPv6 address to a device and you dont have an IPv6 ACL for those services configured then your device might be reachable via IPv6. So even if you haven't started with IPv6 for management and monitoring you have to keep in mind that your router listens on every address and if you have IPv6 enabled on any interface your router might be reachable via IPv6.
Port numbers
The router converts some port numbers to names. This is annoying if you
want to parse and compare that. At least they match up with the services list
published by IANA, altough in some cases the service-name column does not work
and you have to use one of the aliases (e.g. port 80 is www instead of http)
It's just an other piece that makes your parser a bit more complex.
Order of entries in standard ACLs
Standard ACLS are funny. They automagically put single addresses in front of larger prefixes. It looks like those changes are done in a way that does not influence what is permitted and denied by the ACL, but it makes some things hard to read, because now everything is out of order.
Entering
ip access-list standard order1
permit 10.0.0.0 0.0.0.255
permit host 10.0.42.0
results in this config:
ip access-list standard order1
permit 10.0.42.0
permit 10.0.0.0 0.0.0.255
But because that is not confusing enough, you can always add remarks to make things easier to understand...
These commands
ip access-list standard order2
permit 10.0.0.0 0.0.0.255
remark test1
Result in the expected config:
ip access-list standard order2
permit 10.0.0.0 0.0.0.255
remark test1
Add an other address, e.g. this:
permit 10.0.42.0
And your config now looks like this:
ip access-list standard order2
remark test1
permit 10.0.42.0
permit 10.0.0.0 0.0.0.255
This is because the remark is always attached to the line after it (not adding a line after it is probably a corner case) and when the single address is added it is attached to this line. But single addresses are put to the top and the remark with them.
Putting one remark in front of several entries can screw you up beautifully.
In this example we have 2 groups, called group1 and group2
Each group has a single address and a prefix in it.
One could now build an ACL that looks like this.
ip access-list standard out-of-order
remark group1
permit 10.0.1.0 0.0.0.255
permit 10.0.0.0
remark group2
permit 10.0.2.0
permit 10.0.3.0 0.0.0.255
What ends up in the config is this:
ip access-list standard out-of-order
remark group2
permit 10.0.2.0
permit 10.0.0.0
remark group1
permit 10.0.1.0 0.0.0.255
permit 10.0.3.0 0.0.0.255
It looks like the groups have switched positions and 10.0.0.0 and
10.0.3.0 0.0.0.255 have changed groups.
Good luck reverse engineering ancient firewall rules...
The sequence numbers in IOS-XE 16.12 can explain what happens here.
ip access-list standard out-of-order
30 remark group2
30 permit 10.0.2.0
20 permit 10.0.0.0
10 remark group1
10 permit 10.0.1.0 0.0.0.255
40 permit 10.0.3.0 0.0.0.255
Connecting to a Device via SSH from Netbox
2020-11-08
Connecting via SSH to a device in netbox would be nice. So I build a thing.
Keep in mind that you have to adjust almost every config or script to your environment.
First of all you need a custom link for devices in netbox that somehow encodes the hostname of your device in a URL.
So your URL could look like this:
ssh://{{ obj.name }}.example.com
An when you give it a name like
{% if obj.device_role.name == "Router" %}SSH Login{% endif %}
the link is only shown to devices with the router role.
When you click on the link your browser should ask you how to open it.
Now you can build a little script that parses that url, opens your favorite terminal
and starts ssh in there. My script is called sshterminal.
Dont forget to set execute permissions on the script.
#!/bin/bash
HOST=$(echo "$1" | cut -d"/" -f 3)
alacritty -e ssh $HOST
alacritty is currently the terminal of my choice, but any terminal that has an
option to directly execute a programm should work.
(thats what the -e option does.)
If something else opens that url you have to set up your browser to use the
script.
In firefox that is somewhere in the "applications" menu in about:preferences#general.
Now you have a terminal with an ssh connection to the device.
You probably also want to have some options like jump hosts, ancient ciphers for shitty routers, a username and an ssh key. So put something like this in your ssh config:
host *.example.com
user admin
Ciphers=+aes256-cbc
KexAlgorithms=+diffie-hellman-group14-sha1
IdentityFile=~/.ssh/my_private_key
ProxyJump my_jump_host
Weechat setup for IRC in tmux via SSH
2020-09-12
Joining some IRC channels was something that I wanted to do for a long time. But just using a regular client on my laptop does not work, because IRC does not store messages for later delivery. Since my Laptop is often not connected to the IRC server for various reasons I had to find a workaround for that. So I gave the Weechat + tmux + ssh setup a try.
I started with a debian VM that is online 24/7. Then I installed Weechat and tmux:
apt install weechat-curses weechat-plugins tmux
Now I needed a user to log in as via SSH and to run Weechat. After that lingering has to be enabled so that the user is allowed to run systemd user services while not being logged in.
loginctl enable-linger $USERNAME
The systemd service is basically copied from the Arch Linux Wiki and looks like this:
[Unit]
Description=A WeeChat client and relay service using Tmux
After=network.target
[Service]
Type=forking
RemainAfterExit=yes
ExecStart=/usr/bin/tmux -L weechat new -d -s weechat weechat
ExecStop=/usr/bin/tmux -L weechat kill-session -t weechat
[Install]
WantedBy=default.target
This unit file is stored as ~/.config/systemd/user/weechat.service
The important part is the tmux -L weechat in the commands in the unit file.
For reasons explained further in the Arch Linux wiki article the way systemd
starts services would kill the tmux session in which weechat is started
after startup. With -L weechat a socket called weechat is used instead of
default one which is not impacted by the systemd behavior.
To enable and start the service use
systemctl --user enable weechat.service
systemctl --user start weechat.service
There should now be a tmux sesson with Weechat inside.
Connecting to it is possible via tmux -L weechat attach
To make sure that systemd works as intended reboot the VM and check again.
After that some work has to be done to make it easier to access the tmux session. I started with a script like this on the server:
#!/bin/bash
tmux -L weechat attach
stored in /usr/local/bin/weechat-connect so I dont have to type in the long
tmux command every time.
Then I wanted to start this as if was a regular programm on my laptop. So I made a script
alacritty -e ssh -t <USERNAME>@<SERVER> weechat-connect
and put it somewhere in my path.
alacritty is my terminal emulator, if you use something else just use it.
The -e is just the "run this command" option. I hope that every terminal
emulator has a similar option, just pick the right one.
Running weechat on my laptop attaches me to the WeeChat running in the tmux
session via SSH. Since the SSH connection might die every now and then I might
switch to mosh instead of ssh in the future.
Connecting to a Raspberry Pi at first boot via IPv6 link local addresses
2020-03-07
I installed a Raspberry Pi today.
My problem is that I am lazy and I don't want to take out a HDMI cable and a
keyboard to configure it.
You can configure it via SSH.
To do this you have to create a file called ssh in the boot partition of the
image. 1
But I didn't have a network with DHCP in it.
This is not a problem because the Pi speaks IPv6 and when I plug it directly
into my laptop it does IPv6 router solicitation.
This means that it's address will end up in my laptops neighbor table.
So I can just use ssh pi@fe80::2083:1fb1:2912:d686%enp0s25 and log in as
usual.
Wireguard AllowedIPs caveats
2020-02-15
I recently tried out wireguard.
The AllowedIPs setting confused me a bit.
The name, many blog posts and some parts of the documentation mention that
this setting is some kind of source IP address filter.
But when you have 2 peers in a config that have all addresses allowed you will get errors. An example config for that could look like this (pls forgive me for only using legacy IP in this example):
[Interface]
PrivateKey = < priv key here >
ListenPort = 51820
[Peer]
Endpoint = 172.20.1.104:51820
PublicKey = zfiU3b7CSyTiGZ9YIAOyvKgDHsFsL78Vij6kB9615ys=
AllowedIPs = 0.0.0.0/0
[Peer]
Endpoint = 172.20.1.126:51820
PublicKey = X++p6RAoYuGE0GXiDI+bJbsS0kI9odzwIUpef5nVKRo=
AllowedIPs = 0.0.0.0/0
If the interface is running and you enter a wg show, the result has no
AllowedIPs for the first peer.
interface: wg-p2p
public key: EfGMYv8Vd3DPLzyAKeMtDe6FzU+EVangtMRnkC+urik=
private key: (hidden)
listening port: 51820
peer: zfiU3b7CSyTiGZ9YIAOyvKgDHsFsL78Vij6kB9615ys=
endpoint: 172.20.1.104:51820
allowed ips: (none)
latest handshake: 1 minute, 59 seconds ago
transfer: 180 B received, 284 B sent
peer: X++p6RAoYuGE0GXiDI+bJbsS0kI9odzwIUpef5nVKRo=
endpoint: 172.20.1.126:51820
allowed ips: 0.0.0.0/0
transfer: 0 B received, 3.47 KiB sent
This is because the AllowedIPs setting is not only used as a source filter.
It is also how wireguard decides to which peer a packet is send.
A packet is send to the peer which has the destination address in its AllowedIPs.
The AllowedIPs of peers on an interface can not overlap because wireguard
does not know which of the multiple peers it has to choose.
Each address can only be used once for each interface.
Wireguard does not do routing itself! Adding a longer prefix in the AllowedIPs
does not mean that only this peer will receive the traffic. It means that you
have overlapping addresses configured.
The routing is still done by the linux kernel. The regular routing table needs an entry to send some traffic via the wireguard interface. Only if the routing table decides to send traffic via the wireguard interface the peer config comes into play.
This also means that if you want to build point to point links with wireguard for e.g. for an encrypted, routed backbone you have to create one interface per link. (And not one interface with many peers.)
an Prometheus Exporter for CSGO (and other SRCDS Games)
2019-01-29
I am running the network and/or gameservers for many LAN parties. Once one of the team members told me that some CPUs are to slow to run a CSGO server at 128 ticks per second. Verifying that this happens was not that easy because back then he only had a couple of commands he could execute on the command line of the client. This means that he could only verify that the server is running fast enough while actually being on the server. This is not possible during matches.
Somewhen I stumbled across srcds_perfmon.
I actually never used the software.
But it has shown me the stats command for SRCDS.
This command prints out several statistics, e.g. the tickrate of the server,
network traffic, number of maps played and several others.
Sadly the output is not consistent between different kinds of servers.
CSGO for example outputs
CPU NetIn NetOut Uptime Maps FPS Players Svms +-ms ~tick
10.0 0.0 0.0 8967 0 63.80 0 5.22 0.25 0.05
while L4D2 does not have all of those fields. An other issue is that those fields are not documented. Here is a annotated list which I made from observation, tests and guesses:
- CPU - unknown
- NetIn - inbound network traffic in kbit/s
- NetOut - outbound network traffic in kbit/s
- Uptime - uptime of the server in minutes
- Maps - number of maps played
- FPS - the tickrate of the server
- Players - the number of real players, bots are not counted
- Svms - unknown
- +-ms - unknown
- ~tick - unknown
If you find mistakes in this list feel free to contact me.
Now to the monitoring part.
Since Prometheus is used on many of the events I am
helping I wrote an exporter for prometheus.
Connecting to a gameserver is often solved via RCON
which allows you to execute commands on the gameserver and retrieve the output.
I am using the python library aiorcon for this.
I am not only executing the stats command but also the status command.
status returns some further information not included in stats e.g. the
servers name, the amount of bots and the maximum amount of players allowed on
the server.
The name of the server is used as a label and might be used in dashboards.
To handle the webserver part which is facing to prometheus I used aiohttp, an asynchronous webserver for python. The whole exporter completely follow the recommendations for prometheus exporters. It does not have to run once per gameserver on the same machine. It can be run on any server because it makes no difference where it is running from the query perspective. Also on some events the gameserver people don't know how to handle such an exporter. Therefore just giving the monitoring guy the rcon password and address is sufficient. Also you can easily monitor servers on which you have no direct access, e.g. when the server is run by some hoster which does not allow you to execute random code on his servers. One exporter can therefore query many servers.
Putting the password into the exporter requires a little trick with the relabeling
configs of prometheus.
Instead of defining targets as <addr>:<port> they are defined as <addr>:<port>:<rcon_pw>.
The password is generated via a regex from the given target specification.
Then the target specification is rewritten to remove the :<rcon_pw> part.
The full relabeling config and the source code can be found in the github repository.
I later realized that someone build a similar exporter
before which sadly has the same name and does only
use the status command and does therefore not have the performance metric support.
Updating a HP SE326M1 Server
2018-10-08
I have an old HP SE326M1 server. According to rumors on the internet those servers are a OEM version of the DL180G6 with 25 2.5" drives and were used in Microsoft datacenters.
Anyway, I wanted to use this server again. One issue I had with this server was that the combination of the SAS backplane and the RAID controller have an issue. When using the cli tool from within Linux to configure the RAID controller all disks are shown in slot 0. This means that you can not create or modify arrays because the controller (at least from within the Linux cli tool) can not distinguish the different drives. A long time ago I heard that a firmware upgrade was required.
So I set out to find the firmware upgrade.
Somewhen I stumbled over a SPP from HP. This is the "Server Pack for Proliant"
which contains the firmware upgrades for the HP server.
Normally these SPPs require a active support contract. But I found one on the HP
website which did not. If can't find that SPP you may ask someone else who has
access to one e.g. someone who is working for a company with HP servers.
I downloaded this file after creating an account to download this firmware pack.
(WTF HP!? why do I need an account to download a firmware package?).
After downloading a 5.6GB iso file (WTF HP!?) with only 3MB/s (WTF HP!?) which
took about 30 minutes I tried what every mentally sane Linux guys would do:
use dd to copy the image to a usb stick.
This did not boot at all.
So I went to long way , booted up windows, copied the 5.6GB file to a USB stick,
mounted the iso on windows and used the hpusbkey.exe tool to build a usb stick with
that tool.
The tool copied all the files and then just crashed.
Anyways I tried booting it anyway.
But after booting that I just got the message that the boot failed and that
pressing any key would reboot the system.
Okay, this did not work.
The next place to try out was iLo2. This is HPs remote management tool. So after several failed attempts to configure an IP address either static or via DHCP I was close to throwing the server out of the window. Then I reseted the iLo config completely and suddenly it accepted IPs via DHCP.
Now there was the next problem: When connecting to the ilo you get a
SSL_BAD_HMAC_ERROR, which means that something is broken with SSL/TLS.
A workaround is to change some settings of firefox in about:config.
The required key is called security.tls.version.fallback-limit.
If you set this to 1firefox is talking with ilo2.
But be carefull, this enables fallbacks from newer TLS versions to older ones
which makes some MITM attacks which involve falling back to older SSL/TLS versions
possible.
Upgrading iLo2 to the most recent firmware version was working very well. The firmware can be found for example (here)[http://pingtool.org/latest-hp-ilo-firmwares/]. This page also describes how to get the bin file extracted from the .scexe file HP gives you. Somewhere in the Administration tab you can find a firmware upgrade section. Just upload the firmware there and wait a minute for the iLo to reboot.
Now starts the funny part. iLo2 uses Java applets for remote media mounting and for the remote console. All major browsers removed the support for Java applets. Even the current firefox extended support release got rid of it by now. Someone on (reddit)[reddit.com] mentioned a browser called PaleMoon which still supports it but I haven't tryed that yet. The solution that I ended up with was using Windows 7 and the Internet Explorer 11. This works because iLo2 also has an implementation specificly for IE. This way I was able to mount the SPP iso image on the server and managed to boot from that. But this takes ages. First it needs ~1 minute to boot. Then you have to select if you want to run it in automatic or interactive mode. I chose the automatic mode by accident which worked out. Then it copies things to memory. This took 10-15 minutes for me. Then I reached some kind of GUI with a blue background. At least I had a mouse now. After an other 15 minutes it loaded something which looked like a browser window. At least it pretended to be waiting to transfer some data from 127.0.0.1. After an other 10 minutes the page loaded and started analysing the system. Then it showed a page and was scanning for the firmware upgrades and applied some of them. After a sudden reboot the backplane and raid controller firmware were up-to-date.
installing the hpucacli or ssacli utilies
hpacucli which was later renamed to hpssacli which is now known as ssacli is a tool to access the HP RAID controllers from within the operating system. Sadly this is not in the official repositories but HP has a repository for debian which is maintained for the current (stretch) release.
Furter details on how to install this can be found here. If you have issues with installing take a look at the comment section of this page. I will keep it short and add the commands I used here.
echo -e "deb http://downloads.linux.hpe.com/SDR/repo/mcp/ stretch/current non-free" > /etc/apt/sources.list.d/proliant.sources.list
apt install dirmngr
apt-key adv --keyserver keyserver.ubuntu.com --recv-keys C208ADDE26C2B797 # this is adding the required key from a repo server.
apt update
apt install ssacli
Snake was fun, but Tetris is better!
2018-06-13
A couple of weeks ago I make a snake clone. Then I made Whac-a-Mole and now I stopped at Tetris.
You can find this and the other games here.
Like the last games this one is also build with jQuery, Javascript, HTML and CSS.
This game was a lot more painful to write, because there are several boundary
checks at serveral positions. Also I ran into some interesting bugs which makes me
more careful when using the || operator.
Often this is used like this
a = a || default_value;
to asign default values if no value is given. This works due to JS values being
truthy or falsy. The || operator takes the first truthy value and returns this.
Basically as long as a is not null, undefined or false one gets the left value.
But there are more falsy values.
There are also 0, -0, NaN and empty strings like "", ''
(to be accureate the specs say every string of length 0 is falsy).
While digging deeper I realized that there are some further caveats, this
stackoverflow answer sums them up.
In conclusion: You have to be careful when using this operator because you could
get a 0 or an empty string as an input which might screw you, because this might
have been a value which you wouldn't want to replace.
My workaround looks like this:
if(rotation === undefined){
rotation = current_tetromino.rotation;
}
rotation is a parameter of the function that contains this code and has undefined
as a default value. This works but there are probably some nicer versions.
Maybe this one is better, but still looks very clumsy due to the long variable names.
rotation = (rotation === undefined) ? current_tetromino.rotation : rotation;
A with shorter names it looks like this:
rot = (rot === undefined) ? cur.rot : rot;
This is a bit shorter, but the ternary operator still looks a bit weird to me. I never really liked that fellow but peerhaps I should use it every now and then.
Okay, back to the game. There is still something left to do: I want to change the way the field is drawn. Currently the complete field is redrawn every time something changes. It feels a bit slow sometimes, especially when you rotate a tetromino (thats the name of a block) twice. Most of the time at most 8 grid cells need to be adjusted. When the player fills one or more lines those lines need to be deleted and everything from that point upwards needs to be drawn again.
I made a snake clone part 2
2018-05-23
In my last post I wrote about the snake clone I have written.
With some feedback I got from a couple of friends I added some features to make the game more interesting.
First of all every 10 points the game spawns a stone on the field. The stone is an other obstacle which the snake is not allowed to run into. If you do, you lose a life. The stones are only generated on positions where there is no food or the snake and are at least 4 blocks away from the head of the snake. (Pythagorean theorem fuck yeah!)
The second adjustment I made is to increase the games speed over time. I initially wanted to change the game speed whenever some food is eaten. But since coding, testing and thinking about what you are actually doing hasn't worked out I changed the game speed every step the game does. After a couple of games I realized what I had done and I like the mechanic because it rewards a more aggressive playstyle which collects the food in a faster fashion than allways taking a nice way which gets your snake out of the way and keeps the field open. Especially with a formula like
timestep = timestep * 0.97
the game got pretty fast pretty fast. At ~30 points the game was to fast to be played by a human. Other values like 0.995 moved that point further away but were not really motivating because the game still got insanly fast. So I had to limit the speed of the game to some level that is still playable but not demotivating. I came up with
timestep = basestep * (0.5 + e**(-0.01*step)/2)
basestep is the starting speed of the snake. By default this 333ms.
step is the amount of steps the game has done so far. This is basically how often
your snake has moved yet.
e**(-0.01*step)/2 decreases from 0.5 to 0 for large step counts.
Together with the 0.5 this results in a timestep that decreases from basestep
to 0.5*basestep.
For example after 500 steps the total speed is at ~0.506*basestep or about
twice as fast as at the beginning.
Also the game can now be played here.
I made a snake clone
2018-05-18
Today I procrastinated and build a snake clone with HTML, CSS, JavaScript and jQuery.
You can play it here
All together the game has ~200 lines of code. Everything runs in the browser, no fancy server needed. I used the CSS flexbox for many things and wrote my own little "library" for the grid layout.
I am thinking about adding some stones or something in the way to make the game harder. Other options would be some powerups that increase how many points you gain or make the snake faster/slower/shorter. An other idea would be to make this a multiplayer game with the goal to enclose the other player.
Also I am thinking about making more games based on the grid library.
Spontaneous ideas are:
- tetris
- whac-a-mole
- 2048
I don't know what the future might bring. Have fun playing.
Importing music with beets (part 1)
2018-05-02
beets is a tool for organizing music. It can auto import your music collection. But the auto import feature is missing some things in my opinion. I will work around some of it's limitations and report on the progress.
The currenct circumstances are:
- I have a lot of music sorted in different ways.
This means that I have multiple harddisks/folders with music on them.
Each of them might be sorted differently, e.g. one with
$artist/$album/$number - $titleand an other one with$artist - $album/$title. Some folders contain music that is also in others. Some may contain full albums, others might not. Some folders may contain the same song in a different file format Some folders may also contain non-music files, e.g. the cover art, log files from converting to an other file format or just other random things. - I want to sort my music collection in one place, sorted by
$artist/$album/$number - $title - I want to have everything just once
- I have ~30000 tracks in my collection that are already imported into beets and sorted properly.
- I have several 100GB of music laying around that has to be sorted.
- I want to do as less as possible by hand, because a manual approach does not scale well.
- I am not afraid to lose some of the things that are somewhere on some harddisk because the difference between not finding them because I am to lazy to search several disks and not having them is not relevant from a practical perspective.
Okay, let's dive into the sorting process.
beets settings
Everything I have changed in the beets settings (~/.config/beets/config.yaml) is
directory: /data/music/library/
library: /data/music/library.blb
import:
move: yes
the first two lines are where my music library will be stored and the second line defines where the database which is used by beets is stored. The relevant setting for me is the fourth line. This tells beets to move files into the library folder which leaves me with folders that do not contain music files anymore
Automatic importing
First I am running beets automatic import feature over everything. The important point is to create a logfile, because this will help us with duplicates.
The command do this with is: beet import -q -l import.log
Removing duplicates
beets can find duplicates but it does not automatically remove them. We will take care of those duplicates now with the log file we made with the last step. The logfile now says something like this:
import started Wed May 2 15:05:42 2018
skip /data/music/F/F.R. - Mixtape
skip /data/music/F/FAME - Real Talk Mixtape
skip /data/music/F/FaSy - 33
skip /data/music/F/Fabricant - Demo 2010
skip /data/music/F/Face Of Ruin - Within The Infinite
skip /data/music/F/Faeces - Upstream
skip /data/music/F/Fail Emotions - 2009 - Side A
skip /data/music/F/Fail Emotions - 2010 - Dance Macabre
skip /data/music/F/Fail Emotions - 2010 - Make Bad
skip /data/music/F/Falconer - 2003 - The Sceptre Of Deception
duplicate-skip /data/music/F/Fall Out Boy - Infinity On High
skip /data/music/F/Fall Out Boy - Take This To Your Grave-Direct
skip /data/music/F/Farin Urlaub - Am Ende der Sonne
skip /data/music/F/Farin Urlaub - Die Wahrheit übers Lügen
skip /data/music/F/Farin Urlaub - Endlich Urlaub
skip /data/music/F/Farin Urlaub - Livealbum of Death
skip /data/music/F/Farin Urlaub - Porzellan
skip /data/music/F/Fasics - Ich tu was ich kann! - EP
duplicate-skip /data/music/F/Fear Factory - Archetype (2004) [320KB]
skip /data/music/F/Fear Factory - Demanufacture (1995) [320KB]
duplicate-skip /data/music/F/Fear Factory - Demanufacture [Remastered] (2005) [320KB]
duplicate-skip /data/music/F/Fear Factory - Digimortal (2001) [320KB]
skip /data/music/F/Fear Factory - Mechanize (2010) [320KB]
skip /data/music/F/Fear Factory - Transgression (2005) [320KB]
... [chopped of here]
All lines that started with duplicate-skip have automatically been detected as
duplicates.
They are not needed anymore and can be removed.
A simple bash one-liner for this could look like this:
grep "^duplicate-skip" import.log | cut -d" " -f2- | while read line; do rm -r "$line"; done
First we find all lines that start with duplicate-skip, then we chop of the duplicate-skip
to get the path.
Then we delete each of the duplicates.
Since building one-liners is dangerous I would first start with
grep "^duplicate-skip" import.log | cut -d" " -f2- | while read line; do echo rm -r "$line"; done
The little but important difference lies in the echo.
This prints all the rm -r that would be executed into the shell to check them manually
and prevent major skrew ups.
When everything looks fine.
In my case it looks like this:
rm -r /data/music/F/Fall Out Boy - Infinity On High
rm -r /data/music/F/Fear Factory - Archetype (2004) [320KB]
rm -r /data/music/F/Fear Factory - Demanufacture [Remastered] (2005) [320KB]
rm -r /data/music/F/Fear Factory - Digimortal (2001) [320KB]
rm -r /data/music/F/Finntroll - Jaktens Tid
rm -r /data/music/F/Finntroll - Jaktens Tid (2001)
rm -r /data/music/F/Finntroll - Midnattens Widunder (1999)
rm -r /data/music/F/Finntroll - Nattfodd (2004)
rm -r /data/music/F/Finntroll - Nattfödd
rm -r /data/music/F/Finntroll - Trollhammaren (2004)
rm -r /data/music/F/Finntroll - Ur Jordens Djup
rm -r /data/music/F/Finntroll - Visor Om Slutet (2003)
rm -r /data/music/F/For The Fallen Dreams - Back Burner 2011
rm -r /data/music/F/For The Fallen Dreams - Changes
rm -r /data/music/F/For The Fallen Dreams - Wasted Youth (2012)
rm -r /data/music/F/For the Fallen Dreams - Relentless
rm -r /data/music/F/Fort Minor - The Rising Tied
rm -r /data/music/F/Frithjof Brauer - Nevertheless
rm -r /data/music/F/Frithjof Brauer - Tales from the past
rm -r /data/music/F/From Autumn to Ashes - Holding a Wolf by the Ears
rm -r /data/music/F/From Autumn to Ashes - The Fiction We Live
rm -r /data/music/F/From Autumn to Ashes - The Fiction We Live_
rm -r /data/music/F/From Autumn to Ashes - Too Bad You're Beautiful_
rm -r /data/music/F/Funeral for a Friend - Hours
rm -r /data/music/F/Funeral for a Friend - Memory and Humanity
rm -r /data/music/F/Funeral for a Friend - Seven Ways to Scream Your Name
rm -r /data/music/F/Funeral for a Friend - Tales Don't Tell Themselves
rm -r /data/music/F/Funeral for a Friend - Welcome Home Armageddon
Since these seem to match with the logfile we can probably use the command without
the echo and get rid of the duplicates.
This code has one little corner case: When beets decides to groud to folders together e.g. if you have a 2 CD album with the different CDs in different folders the logfile does something like this:
duplicate-skip path1; path2
This screws up the command with the semicolon.
remove empty directories and other crap
Many of my music folders contain things like cover art, conversion logs or other files. Now it is time to get rid of them. A first and easy approach is to go for file extensions. This is only an approximation because technically the file extension is irrelevant. But it works pretty well.
To find all files I use find
find * -type f -print
This prints all files to the terminal. But we are only interested in the file extension which is everything behind the first dot. I dont care about files that don't have a file extension. They are probably no music files, so they will be deleted later.
find * -type f -name "*.*" -print | rev | cut -d"." -f1 | rev | sort -u > musicfileextensions.txt
The rev command is a little workaround for cut which can only keep the first but
not the last field in which is has split up the input.
The first rev reverses the input, then we cut and keep everything in front of
the first . which was the ending of the files.
The second rev roates our file extensions again.
The sort -u sortes them and removes duplicates.
The > musicfileextensions writes the list to a file.
Now we have a list of all file endings that exist in the directory we are working on.
Mine looks like this:
JPG
MP3
db
gif
ini
jpg
log
m4a
mp3
My list is pretty short because I am only working on a subset of my collection. The final list might be longer.
Now I sadly have to edit this list manually. After removing every non music file extension the list is a little bit shorter.
MP3
m4a
mp3
This shows us something which is pretty annoying: People can not decide if the file extension is written in upper- or lowercase letters... We now could care about this and build all commands in a way which ignores the case of letters but since we gathered this list from all our music files this list should be complete and contain all occouring case-sensitive variations.
Time to get rid of some other files. find to the rescue (again)!
We want to delete:
- empty directories
- all files which are no music files (which in our simplified view means all files that dont have on of the music file extensions)
find * -type f ! -name "*.mp3" ! -name "*.MP3" ! -name "*.m4a" -print
find -type d -empty -print
The first command finds all non music files, the second one the directories.
If we append -delete the files/directories are deleted.
Use this with care, first try it without the -delete flag.
find * -type f ! -name "*.mp3" ! -name "*.MP3" ! -name "*.m4a" -print -delete
find -type d -empty -print -delete
Now we got rid of a lot of things (hopefully).
The next steps will be harder and I will talk about them in the next part.
Today I am starting a blog.
2018-03-11
I am not sure what will happen here.